Knotoids

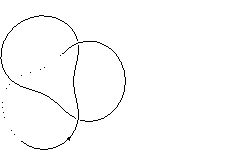
Updated 24^th February, 2021

Here we present some lists of distinct classical and virtual pure knotoids and multi-knotoids in S², as introduced by Vladimir Turaev in [1], with up to 8 crossings. We consider only multi-knotoids with a single segment component as in [1], rather than the generalized concept in [2] that includes multiple segment components. The lists were produced a by computer search based on labelled peer codes, a description of which is available here.

To represent a (multi-)knotoid K using a labelled peer code we add a shortcut that passes everywhere under K, forming K_ in Turaev's notation. Then, K_ is a knot or link for which we can write the labelled peer code determined by numbering the semi-arc containing the leg of K as zero and proceeding in the direction from the leg to the head, backwards along the shortcut (which is also oriented from the leg to the head), then on to any other components that might exist. We identify the first crossing of K_ according to this numbering that involves the shortcut by writing a ^ symbol after the crossing number in the peer code. There is a unique semi-arc that enters this crossing as an under-arc with the orientation of K_ described above. Thus the ^ character uniquely identifies the semi-arc containing the head of K within the segment component of the (multi-)knotoid. Whilst the peer code represents the shortcut with its orientation reversed, this is easily accommodated by the requirement that the peer code numbering always begin with the leg of the knotoid.

Note that this representation of knotoids is only capable of fully describing pure knotoids, since it is not capable of describing a knot-type knotoid produced from a sequentially numbered knot diagram by removing an arc within the edge numbered zero.

The underlying immersion in the plane (the "shadow") of a (multi-)knotoid diagram of K_ described by a labelled peer code is an example of a realizable immersion of a number of copies of S¹ in the plane. The computer search operated by reversing this process, enumerating the closure of knotoids obtained from lists of realizable immersions involving a variety of combinations of the number of components and the number of crossings .

The programme that produced these tables is available as a source distribution here: vlist-release-10-11-20.tar, which requires version 21.0 or later of the braid programme.

The following table shows the number of distinct oriented classical and virtual knotoids, quotiented by the mirror and symmetry involutions, described in [1], identified by the number of (classical) crossings and components. Knotoids are distinguished using the normalized extended bracket polynomial described in [1].

For classical or virtual knotoids having just one component, the normalized extended bracket polynomial is invariant under the reversion involution that interchanges the leg and head of a knotoid. However, it is not invariant under all orientation changes for multi-knotoids, since the sign of a crossing involving two components reverses if the orientation of just one of the components is reversed, impacting the normalizing factor. Moroever, the algebraic number of intersections of the knotoid with the shortcut changes if, for a given choice of shortcut, there is a non-segment component that intersects the shortcut. Similarly, any orientation reverse of such a non-segment component changes the algebraic number of intersections.

Note that the table does not represent all possible distinct knotoids, only those that are distinguished by the normalized extended bracket polynomial and only those for which there is a choice of shortcut such that the closure, K_, may be obtained from one of the realizable immersions considered by the search. The maximum number of crossings in the realizable immersions considered for each set of lists is shown in the row "max shadow immersion crossings". Thus, the lists of single component knotoids were based on realizable immersions of up to 8 crossings, etc.. It may be better, therefore, to regard this table as a lower bound on the number of distinct equivalence classes of knotoids in each case, see the comments following the diagrams below for further details.

The following pages present the labelled peer codes corresponding to the above table:

Classical knotoids

• Classical knotoids with two crossings and one component
• Classical knotoids with two crossings and three components
• Classical knotoids with three crossings and one component
• Classical knotoids with three crossings and two components
• Classical knotoids with three crossings and three components
• Classical knotoids with three crossings and four components
• Classical knotoids with four crossings and one component
• Classical knotoids with four crossings and two components
• Classical knotoids with four crossings and three components
• Classical knotoids with four crossings and four components
• Classical knotoids with five crossings and one component
• Classical knotoids with five crossings and two components
• Classical knotoids with five crossings and three components
• Classical knotoids with five crossings and four components
• Classical knotoids with six crossings and one component
• Classical knotoids with six crossings and two components
• Classical knotoids with six crossings and three components
• Classical knotoids with six crossings and four components
• Classical knotoids with seven crossings and one component
• Classical knotoids with seven crossings and two components
• Classical knotoids with seven crossings and three components
• Classical knotoids with seven crossings and four components
• Classical knotoids with eight crossings and two components
• Classical knotoids with eight crossings and three components
• Classical knotoids with eight crossings and four components

Virtual knotoids

• Virtual knotoids with two crossings and one component
• Virtual knotoids with two crossings and two components
• Virtual knotoids with two crossings and three components
• Virtual knotoids with three crossings and one component
• Virtual knotoids with three crossings and two components
• Virtual knotoids with three crossings and three components
• Virtual knotoids with three crossings and four components
• Virtual knotoids with four crossings and one component
• Virtual knotoids with four crossings and two components
• Virtual knotoids with four crossings and three components
• Virtual knotoids with four crossings and four components
• Virtual knotoids with five crossings and one component
• Virtual knotoids with five crossings and two components
• Virtual knotoids with five crossings and three components
• Virtual knotoids with five crossings and four components
• Virtual knotoids with six crossings and one component
• Virtual knotoids with six crossings and two components
• Virtual knotoids with six crossings and three components
• Virtual knotoids with six crossings and four components
• Virtual knotoids with seven crossings and two components
• Virtual knotoids with seven crossings and three components
• Virtual knotoids with seven crossings and four components

The following classical knotoids are those having up to 5 crossings that are distinguished by Turaev's extended bracket polynomial, described in [1]. The diagrams below have been produced automatically using the draw programme. It has not yet been possible to create aesthetic normalized knotoid diagrams, where the leg is in the unbounded component of the diagram's compliment, using this approach.

k2.1.1 labelled peer code: [-3 -5^ -1]/+ + +
Extended bracket polynomial: −A¹⁰u²+A⁶u²+A⁴

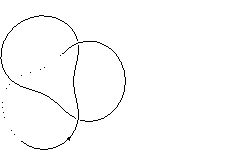
k3.1.1 labelled peer code: [-3 5 -7^ 1]/+ + + +
Extended bracket polynomial: A⁻⁸−A⁻⁴−A⁻²u²+A²u²+1

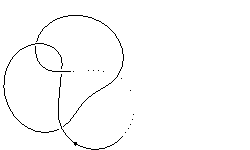
k4.1.1 labelled peer code: [-3 -7 -9^ -1 -5]/+ + + + +
Extended bracket polynomial:  −A¹⁸u²−A¹⁶+A¹⁴u²+2A¹²−A⁸+A⁴

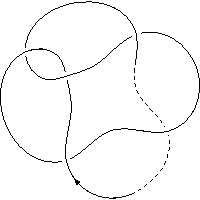
k4.1.2 labelled peer code: [-5 -7 -9^ -3 -1]/+ + + + +
Extended bracket polynomial:  −A¹⁸u²+A¹⁴u²+A¹²−A¹⁰u²−A⁸+A⁶u²+A⁴

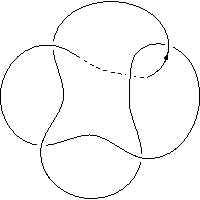
k4.1.3 labelled peer code: [-5 -7 -9^ -1 -3]/+ + + + +
Extended bracket polynomial:  −A²²u²+A¹⁸u²−A¹⁴u²+A¹⁰u²+A⁸

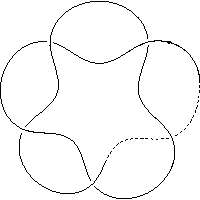
k4.1.4 labelled peer code: [-3 -11 -1 -9 -5 -7^]/+ + + + + -
Extended bracket polynomial:  A²⁰−2A¹⁶−A¹⁴u⁻²−A¹⁴u²+A¹²+A¹⁰u⁻²+A¹⁰u²+A⁸

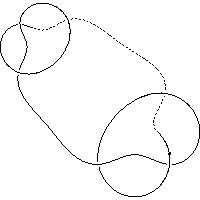
k4.1.5 labelled peer code: [-3 -11 -1 -9 -5 -7^]/+ + + - - -
Extended bracket polynomial:  −A⁻⁶u⁻²−A⁶u²−A⁻⁴−A⁴+A⁻²u⁻²+A²u²+3

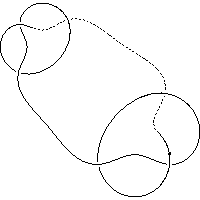
k4.1.6 labelled peer code: [-3 -11 -1 9 5 7^]/+ + + + + -
Extended bracket polynomial:  −A⁻⁶u²−A⁶u²−A⁻⁴u⁴−A⁴u⁴+A⁻²u²+A²u²+2u⁴+1

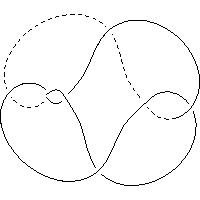
k4.1.7 labelled peer code: [-3 -11 -1 9 5 7^]/+ + + - - -
Extended bracket polynomial:  A²⁰u⁴−2A¹⁶u⁴−2A¹⁴u²+A¹²u⁴+2A¹⁰u²+A⁸

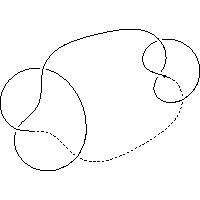
k4.1.8 labelled peer code: [-7 -5 9 -11 -1 3^]/+ + + + + -
Extended bracket polynomial:  A¹⁴u²−2A¹⁰u²−A⁸u⁴+A⁶u²+A⁴u⁴+A⁴

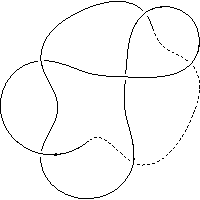
k4.1.9 labelled peer code: [5 -9 -7 11 -1 -3^]/- + + + + -
Extended bracket polynomial:  −A¹⁶u⁻⁴−A¹⁴u⁻²+A¹²u⁻⁴+A¹⁰u⁻²+A⁸

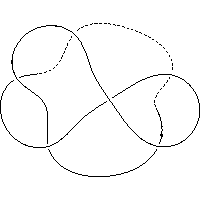
k4.1.10 labelled peer code: [-7 -5 9 -11 -1 3^]/- + + + - -
Extended bracket polynomial:  −A⁻¹²u⁴−A⁻¹⁰u²+A⁻⁸u⁴+2A⁻⁶u²+A⁻⁴−A⁻²u²

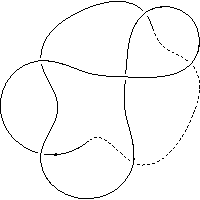
k4.1.11 labelled peer code: [5 -9 -7 11 -1 -3^]/- - + + - -
Extended bracket polynomial:  −A⁶u⁻²−A⁻⁴u⁻⁴+A²u⁻²+u⁻⁴+1

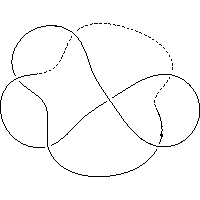
k5.1.1 labelled peer code: [-3 -11^ -1 -9 -5 -7]/+ + + + + +
Extended bracket polynomial:  A²⁶u²−2A²²u²−A²⁰+A¹⁸u²+A¹⁶−A¹⁴u²+A¹⁰u²+A⁸

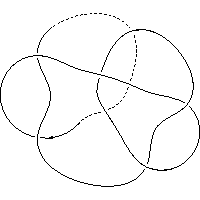
k5.1.2 labelled peer code:[-9 -5 -1 -3 -11^ -7]/- + + + + +
Extended bracket polynomial:  −A¹⁶+A¹²+A⁴

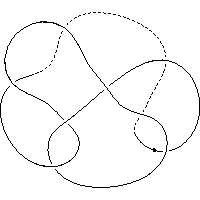
k5.1.3 labelled peer code: [-9 -5 -1 -3 -11^ -7]/- + + + + -
Extended bracket polynomial:  −A¹²−A¹⁰u²+A⁸−A⁻⁶u²+2A⁶u²+A⁻²u²−A²u²+1

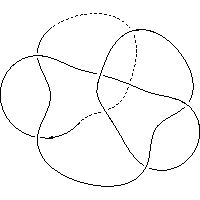
k5.1.4 labelled peer code:[-3 7 -11^ -9 1 -5]/+ + + + + +
Extended bracket polynomial:  A¹⁰u²+A⁻⁸+A⁸−A⁶u²−A⁻⁴−2A⁴+2

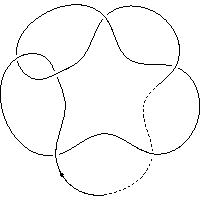
k5.1.5 labelled peer code: [5 -9 -7 11^ -3 -1]/+ + + + + +
Extended bracket polynomial:  A¹⁶−A¹²−A¹⁰u⁻²+A⁸+A⁶u⁻²−A⁴+A⁻²u⁻²−A²u⁻²+1

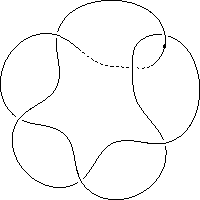
k5.1.6 labelled peer code: [-3 7 -9 -11^ 1 -5]/+ + + + + +
Extended bracket polynomial:  A¹⁴u²−2A¹⁰u²+2A⁶u²+A⁻⁴+A⁴+A⁻²u²−2A²u²−1

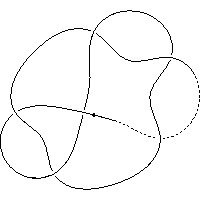
k5.1.7 labelled peer code: [5 -7 -9 11^ -3 -1]/+ + + + + +
Extended bracket polynomial:  A²⁰−2A¹⁶−A¹⁴u⁻²+2A¹²+A¹⁰u⁻²−A⁸−A⁶u⁻²+A⁴+A²u⁻²

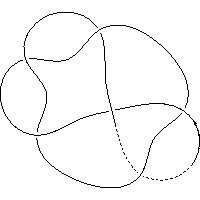
k5.1.8 labelled peer code: [-5 -7 9 -1 -11^ 3]/+ + + + + +
Extended bracket polynomial:  A¹⁴u²−2A¹⁰u²−A⁸+2A⁶u²+A⁻⁴+2A⁴−A²u²−1

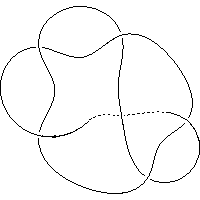
k5.1.9 labelled peer code: [-5 -7 9 -1 -11^ 3]/- - + - + +
Extended bracket polynomial:  −A⁻²⁴−A⁻²²u²+A⁻²⁰+2A⁻¹⁸u²−2A⁻¹⁴u²+A⁻¹⁰u²+A⁻⁸

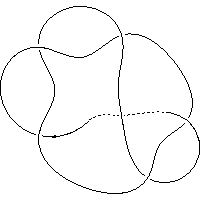
k5.1.10 labelled peer code: [-3 -7 9 -1 11^ 5]/+ + + + + +
Extended bracket polynomial:  −A¹²+2A⁸−A⁻⁶u⁻²+A⁶u⁻²−2A⁴+2A⁻²u⁻²−2A²u⁻²+2

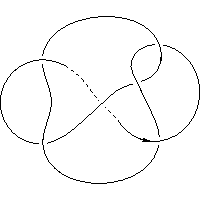
k5.1.11 labelled peer code: [-5 7 -11^ 9 3 -1]/+ + + + + +
Extended bracket polynomial:  −A⁻¹²−A⁻¹⁰u²+2A⁻⁸+2A⁻⁶u²−A⁶u²−A⁻⁴−2A⁻²u²+2A²u²+1

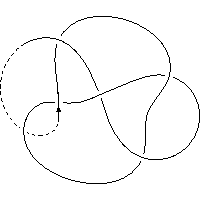
k5.1.12 labelled peer code: [-3 -13 -1 -9 11 -5 7^]/+ + + + + + -
Extended bracket polynomial:  −A¹⁸u²+2A¹⁴u²+A¹²u⁴+A¹²−2A¹⁰u²−2A⁸u⁴−A⁸+A⁴u⁴+A⁴+A²u²

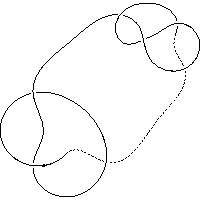
k5.1.13 labelled peer code: [-3 -13 -1 -9 11 -5 7^]/+ + + - - - -
Extended bracket polynomial:  −A¹²u⁴−A¹⁰u²+2A⁸u⁴+3A⁶u²+A⁻⁴−A⁴u⁴+A⁴+A⁻²u²−3A²u²−1

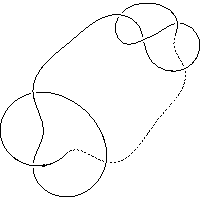
k5.1.14 labelled peer code: [-3 5 -13 1 -11 -7 -9^]/+ + + + + + -
Extended bracket polynomial:  −A¹²−A¹⁰u⁻²+2A⁸+2A⁶u⁻²+A⁶u²+A⁻⁴+A⁻²u⁻²−2A²u⁻²−A²u²−1

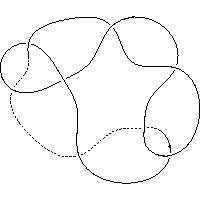
k5.1.15 labelled peer code: [-3 5 -13 1 -11 -7 -9^]/- - + - + + -
Extended bracket polynomial:  −A¹⁸u⁻²+2A¹⁴u⁻²+2A¹²−2A¹⁰u⁻²−3A⁸+A⁶u⁻²−A⁶u²+2A⁴+A²u²

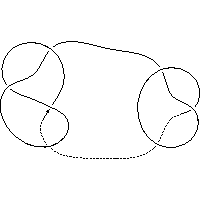
k5.1.16 labelled peer code: [9 13 -7 11 -3 1 5^]/+ + + + + + -
Extended bracket polynomial:  −A⁻¹²−A⁻¹⁰u⁻²+A⁻⁸+2A⁻⁶u⁻²+A⁻⁶u²+A⁻⁴+A⁴−A⁻²u⁻²−A⁻²u²−1

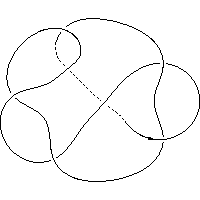
k5.1.17 labelled peer code:[7 11 1 -9 13 -5 3^]/+ - + + + + -
Extended bracket polynomial:  A¹⁰u²+A⁸−A⁶u²−2A⁴+A⁻²u⁻²−A²u⁻²+2

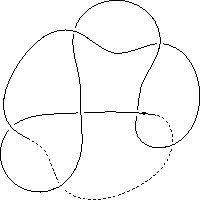
k5.1.18 labelled peer code:[7 11 1 -9 13 -5 3^]/+ - - + + + -
Extended bracket polynomial:  A¹⁴u²+A¹²−2A¹⁰u²−2A⁸−A⁶u⁻²+A⁶u²+2A⁴+A²u⁻²

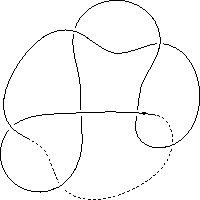
k5.1.19 labelled peer code: [7 11 1 -9 13 -5 3^]/- + + + + + -
Extended bracket polynomial:  A⁸−A⁻⁶u²−A⁶u⁻²−A⁻⁴−2A⁴+2A⁻²u²+A²u⁻²−A²u²+3

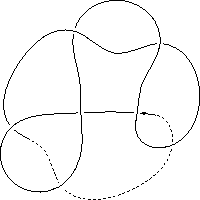
k5.1.20 labelled peer code: [7 11 1 -9 13 -5 3^]/- + - + + + -
Extended bracket polynomial:  A¹⁶−A¹²−A¹⁰u⁻²−A¹⁰u²+A⁶u⁻²+A⁶u²+A⁴

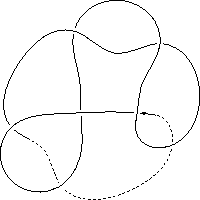
k5.1.21 labelled peer code: [5 9 13 3 -11 1 -7^]/+ + + + + + -
Extended bracket polynomial:  −A⁻¹⁸u⁻²+2A⁻¹⁴u⁻²+A⁻¹²−2A⁻¹⁰u⁻²−A⁻⁸u⁻⁴−A⁻⁸+A⁻⁶u⁻²+A⁻⁴u⁻⁴+A⁻⁴

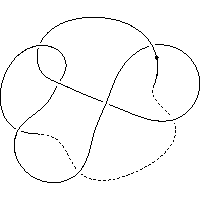
k5.1.22 labelled peer code: [5 9 13 3 -11 1 -7^]/+ + + - + + -
Extended bracket polynomial:  A⁻⁸−A⁶u⁻²−A⁻⁴u⁻⁴−A⁻⁴−A⁻²u⁻²+2A²u⁻²+u⁻⁴+1

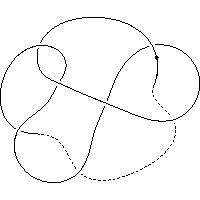
k5.1.23 labelled peer code: [5 9 13 3 -11 1 -7^]/- + + + + + -
Extended bracket polynomial:  A⁻⁸+A⁻⁶u⁻²−A⁻⁴+A⁴u⁻⁴−2A⁻²u⁻²+A²u⁻²−u⁻⁴+1

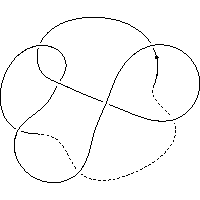
k5.1.24 labelled peer code: [5 9 13 3 -11 1 -7^]/- + + - + + -
Extended bracket polynomial:  −A¹⁰u⁻²+A⁸u⁻⁴+2A⁶u⁻²+A⁻⁴−A⁴u⁻⁴+A⁴+A⁻²u⁻²−2A²u⁻²−1

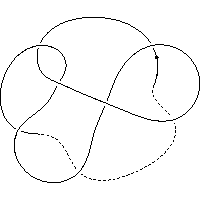
k5.1.25 labelled peer code: [9 13 -7 11 -3 1 5^]/- + + - + - -
Extended bracket polynomial:  −A²⁴+2A²⁰+A¹⁸u⁻²−2A¹⁶−2A¹⁴u⁻²−A¹⁴u²+A¹²+A¹⁰u⁻²+A¹⁰u²+A⁸

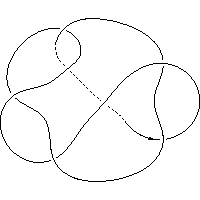
k5.1.26 labelled peer code: [7 -5 11 -9 13 -1 3^]/+ + + + + + -
Extended bracket polynomial:  −A¹²+3A⁸+A⁶u⁻²+A⁶u²+A⁻⁴−2A⁴+A⁻²u⁻²+A⁻²u²−2A²u⁻²−2A²u²

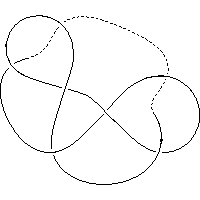
k5.1.27 labelled peer code: [-7 13 -11 -1 3 -5 9^]/- + - - + - -
Extended bracket polynomial:  −A⁻¹⁸u⁻²−A⁻¹⁸u²−A⁻¹⁶+A⁻¹⁴u⁻²+A⁻¹⁴u²+3A⁻¹²−2A⁻⁸+A⁻⁴

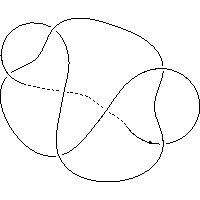
k5.1.28 labelled peer code: [9 -13 -7 11 1 -3 5^]/+ + + + + + -
Extended bracket polynomial:  A⁻¹⁰u²+A⁻⁸−A⁻⁶u²−A⁶u²−A⁻⁴u⁴−2A⁻⁴−A⁻²u²+2A²u²+u⁴+2

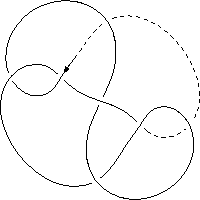
k5.29 labelled peer code: [9 -13 -7 11 1 -3 5^]/- + + + - + -
Extended bracket polynomial:  A¹⁶+A¹⁴u²−A¹²−3A¹⁰u²−A⁸u⁴+2A⁶u²+A⁴u⁴+A⁴

The search algorithm

Starting from a list of labelled peer codes representing distinct link immersions, the search algorithm constructs a list of knotoids by sequentially considering each immersion in the list and assigning labels (positive, negative or virtual as appropriate) to its crossings in all possible combinations. Each set of labels determines a knot or link diagram and gives rise to a number of candidate knotoid diagrams by reversing the above procedure for representing knotoids with labelled peer codes. We consider the leg to be located on the semi-arc numbered zero by the peer code and sequentially assume each crossing to be the head; that is, the first crossing introduced by a shortcut.

The algorithm renumbers each immersion so that each component is numbered first and so that each semi-arc of a component is considered as edge zero. Since the search for multi-knotoids is oriented, this renumbering includes considering all combinations of reversing the orientation of the immersion components in these cases.

For each combination of component order, orientation, choice of starting semi-arc and head, the algorithm checks whether the resultant code is a valid knotoid code. It checks the following conditions.

• The shortcut must lie in the first component of the underlying immersion
• The shortcut must not self-intersect
• The shortcut must pass under the knotoid
• The diagram must represent a pure knotoid

For each valid code we check whether the corresponding diagram may be represented by a diagram with fewer crossings in the underlying immersion, looking for one of the following conditions.

• The first or last crossing of the segment component is virtual
• The diagram is not that of a connected multi-knotoid (the underlying immersion including the shortcut may be connected but the multi-knotoid itself is not)
• A Reidemeister II move is detected between a pair of classical or virtual crossings
• A Reidemeister I move is detected at a classical or virtual crossing
• A Reidemeister I virtual detour is detected at a classical or virtual crossing; that is, a Reidemeister I loop that includes virtual crossings.
• A "turning cycle" virtual detour is detected; that is, a virtual detour between two classical crossings joining edges that both lie in the boundary of the same region of the complement of the underlying immersion.
• A floating virtual component component is detected; that is, one containing only virtual crossings
• A "Gauss virtual detour" is detected; that is, a virtual detour between a pair of classical crossings that may be moved to reduce the number of crossings in the underlying immersion. They are referred to as Gauss virtual detours, since they are detected from the Gauss code for the knotoid by considering sequences of the form:

  ...LiRj...RiLj..., or ...RiLj...LiRj... (standard Reidemeister II parity forwards conditions)

  ...LiRj...LjRi..., or ...RiLj...RjLi... (standard Reidemeister II parity backwards conditions)

  ...LiLj...RiRj..., or ...RiRj...LiLj... (non-standard Reidemeister II parity forwards conditions)

  ...LiLj...RjRi..., or ...RiRj...LjLi... (non-standard Reidemeister II parity backwards conditions)

  ...LiRjRi..., or ...LiLjRi..., or ...RiRjLi..., or ...RiLjLi... ("Reidemeister I"-like conditions)

  When such a condition is detected, count the number of virtual crossings on each of the paths between the ith and jth classical crossing, ignoring those that lie on both paths. If these counts differ sufficiently, then one path may be moved so that it is parallel to the other (with the addition of an extra virtual crossing in the case of the non-standard Reidemeister II, and Reidemeister I configurations) reducing the number of crossings.

  In the case of the standard Reidemeister II conditions, where the crossing labels are compatible, the comparison of the paths takes into account that the two classical crossing themselves may be removed.

• A "virtual Reidemeister II" detour is detected; that is, a condition as above but between a pair of virtual crossings, where one of the paths between the two crossings may be moved to reduce the number of crossings in the underlying immersion.

If a code is not discarded as a result of these checks, then the normalized extended bracket polynomial is calculated and compared with others on our list.

If two knotoids cannot be distinguished by the normalized extended bracket polynomial they belong to the same equivalence class, as determined by that invariant. The algorithm records an example of knotoid having the smallest number of classical non-shortcut crossings, and where possible prefers prime knotoids to connected sums, as a representative of the equivalence class and it is these representatives that are shown in the lists of knotoids above. As examples, the search found 3,703 members of the equivalence class corresponding to the classical knotoid listed as k2.1.1 above, 2,009 members of class k3.1.1, and 1,727 members of class k5.1.3.

One consequence of the search algorithm is that, having distinguished a set of knotoids with k crossings from immersions with n crossings, one cannot discount the possibility of finding another distinct knotoid with k crossings from an immersion having m > n crossings. A classical knotoid K with k crossings will only be encountered by the search algorithm when considering immersions with k+c crossings, where c is the complexity ([1], equivalently the height [2]) of K. A virtual knotoid with k crossings will only be encountered by the search algorithm when considering immersions with k+v+c crossings, where v is the virtual crossing number of the knotoid.

Comparison with original list

The original version of this page, produced in 2015, showed diagrams for the knotoids whose peer codes are given here. This old list has been refined by the latest version of the vlist code and so differs from the lists given above.

In the latest lists, knotoids 4.1.4, 4.1.6 are examples of codes incorrectly rejected by the original search. Including these in the new list of knotoids with four crossings means that knotoids 5.1.14 and 5.1.16 from the original lists are no longer required, since they are indistinguishable from knotoids 4.1.6 and 4.1.4 of the latest list respectively. Also, knotoid 5.1.26 in the new list is an example of a code incorrectly rejected by the earlier search.

References:

[1] V. Turaev, Knotoids, arXiv:1002.4133v4

[2] N. Gugumcu, L. Kauffman, New Invariants of Knotoids, arXiv:1602.0357v3 or European Journal of Combinatorics 65 (2017) pp186-229

[3] N. Gugumcu, L. Kauffman, Parity in Knotoids, arXiv:1905.04089

back to maths homepage